dearbeany
[Java] 다익스트라 알고리즘 (프림과의 차이점, 구현) 본문
1. 다익스트라 알고리즘
- 시작정점에서부터 거리가 최소인 정점을 선택해나가면서 최단경로를 구한다.
- 프림과 유사하나, 프림은 그때그때 선택정점과 인접정점들 중 최소비용 간선인 정점을 선택하는 반면
- 다익스트라는 중간 정점을 들른 비용이 더 작은지 갱신여부를 점검하여 최단경로를 구성한다. (결과적으로 시작정점은 고정)
- 주의점: 다익스트라는 음의 가중치를 허용하지 않는다. (음의 가중치는 벨만-포드 알고리즘을 사용해야 함!)
- shortest path는 사이클을 포함하지 않는다.
- 최단경로 알고리즘의 출력물 ?
d[v] : 최단경로의 weight
p[v] : 최단경로 자체
2. 동작과정
- 시작정점을 입력받는다.
- 거리를 저장할 배열인 dist를 ∞로 초기화한 후 시작점에서 갈 수 있는 곳의 값은 바꿔 놓는다.
- 아직 방문하지 않은 점들이 가지고 있는 값과 현재 정점에서 방문하지 않은 정점까지의 가중치의 합이 작다면 갱신.
(프림과 다른 부분) - 모든 정점을 방문할 때까지 반복한다.
다익스트라 알고리즘을 적용해서 최단경로를 찾아보자.

dist[]: 현재까지 찾은 시작정점으로부터의 최단경로 가중치 (Shortest path weight)
1.a부터 출발
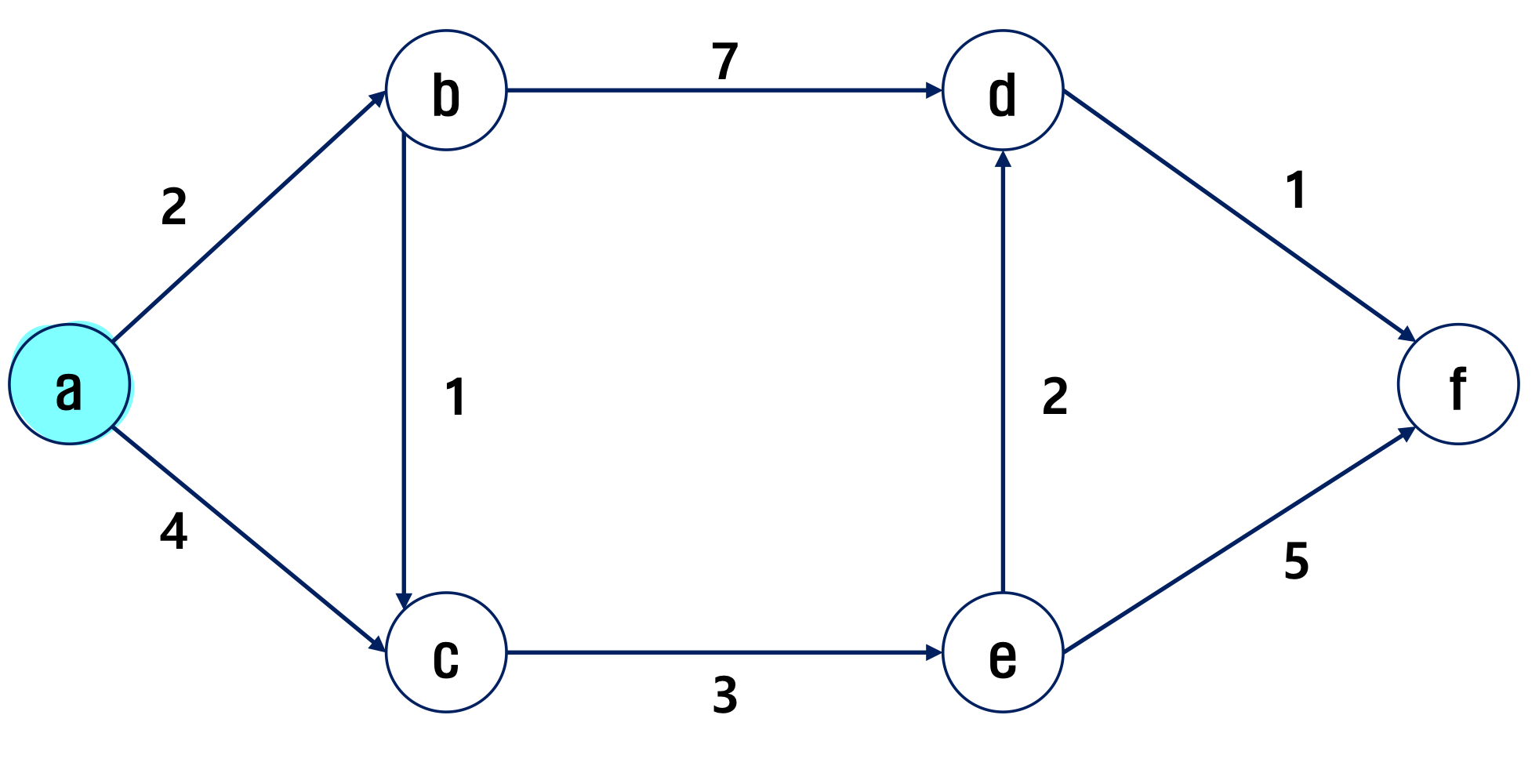
- 시작점의 최소가중치인 dist[a]의 값을 0으로 세팅해준다.
| a | b | c | d | e | f | |
| dist | 0 | ∞ | ∞ | ∞ | ∞ | ∞ |
2. a로부터 갈 수 있는 정점들의 값 갱신
- a와 연결된 정점인 b(2), c(4) dist값을 갱신해준다. 노드(a와 연결된 노드의 가중치)
| a | b | c | d | e | f | |
| dist | 0 | 2 | 4 | ∞ | ∞ | ∞ |
3. 최소값인 b 선택

- b에서 갈 수 있는 노드는 c(1), d(7)이다.
- dist에는 시작정점인 a로부터 해당 정점까지의 최단경로의 가중치가 저장된다. (ex. dist[c] : a부터 c까지 최단경로 가중치)
- 따라서, 현재 dist[c]가 가진 값(= 4, a부터 c까지 간선비용)과 중간정점인 b를 들른 값(a→b→c). (= dist[b] + b와 c의 가중치)를 비교한다.
- dist[c] > dist[b] + c.weight =====> 즉, 4 > 2 + 1 이므로 현재 dist[c]의 값을 더 작은 3으로 갱신.

- 마찬가지로 b와 연결된 노드인 d의 값도 갱신여부를 점검한다.
- dist[d] > dist[b] + d.weight =====> 즉, ∞ > 2 + 7 이므로 현재 dist[d]의 값을 더 작은 9로 갱신.
| a | b | c | d | e | f | |
| dist | 0 | 2 | 3 | 9 | ∞ | ∞ |
cf. 만약 프림일 경우?
| a | b | c | d | e | f | |
| dist | 0 | 2 | 1 | 7 | ∞ | ∞ |
- b와 연결된 c, d의 keys값을 갱신하려고 할 때, 다익스트라와 달리 시작정점인 a기준이 아닌 b를 시작으로 간선의 비용을 비교한다.
4. 최소값인 c 선택

- c와 연결된 정점 중 방문하지 않은 정점인 e(3)의 갱신여부를 점검하자.
- dist[e] > dist[c] + e.weight =====> 즉, ∞ > 3 + 3 이므로 현재 dist[e]의 값을 더 작은 6로 갱신.
| a | b | c | d | e | f | |
| dist | 0 | 2 | 3 | 9 | 6 | ∞ |
5. 최소값인 e 선택

- e와 연결된 정점 중 방문하지 않은 정점인 d(2), f(5)의 갱신여부를 점검하자.
- dist[d] > dist[e] + d.weight =====> 즉, 9 > 6 + 2 이므로 현재 dist[d]의 값을 더 작은 8로 갱신.
- dist[f] > dist[e] + f.weight =====> 즉, ∞ > 6 + 5 이므로 현재 dist[f] = 11로 갱신
| a | b | c | d | e | f | |
| dist | 0 | 2 | 3 | 8 | 6 | 11 |
6. 최소값인 d 선택

- d와 연결된 정점 중 방문되지 않은 f(1)의 갱신여부를 점검하자.
- dist[f] > dist[d] + f.weight =====> 즉, 11 > 8 + 1 이므로 dist[f] = 9
| a | b | c | d | e | f | |
| dist | 0 | 2 | 3 | 8 | 6 | 9 |
3. 인접리스트 & 우선순위 큐를 활용한 다익스트라 구현
/*
* 1. 거리가 저장되는 배열 dist를 무한대로 세팅
* 2. 임의의 정점으로부터 시작. dist[시작점]=0. 시작노드는 PQ에 넣어주기
* 3. PQ(정렬기준이 명시된)에서 시작노드를 꺼내면서 인접노드들 탐색 (단, 이미 방문한 건 패스)
* 4. 최단경로의 비용으로 갱신하자
* - 인접노드의 dist > 현재노드의 dist + 인접노드의 값 이라면 갱신
* 5. 갱신한 값이 담긴 노드를 다시 큐에 넣어주기
*/
public class Main {
static class Node implements Comparable<Node> {
int v, weight;
public Node(int v, int weight) {
this.v = v;
this.weight = weight;
}
@Override
public int compareTo(Node o) {
return Integer.compare(this.weight, o.weight);
}
}
static final int INF = Integer.MAX_VALUE;
static int V, E; // V : 정점 , E : 간선
static List<Node>[] adjList; // 인접리스트
static int[] dist; // 최단 길이를 저장할 값들.
public static void main(String[] args) {
Scanner sc = new Scanner(input);
V = sc.nextInt(); // 0번부터 시작
E = sc.nextInt();
adjList = new ArrayList[V];
for (int i = 0; i < V; i++)
adjList[i] = new ArrayList<>();
dist = new int[V];
Arrays.fill(dist, INF);
/////////////////////////////// 초기화 완료
for (int i = 0; i < E; i++) {
int st = sc.nextInt();
int ed = sc.nextInt();
int w = sc.nextInt();
// 유향 그래프
adjList[st].add(new Node(ed, w)); // 인접 리스트에 넣기
} // 입력끝
dijkstra(0);
System.out.println(Arrays.toString(dist));
}
private static void dijkstra(int st) {
PriorityQueue<Node> pq = new PriorityQueue<>();
boolean[] visited = new boolean[V]; // 방문처리 용도
pq.add(new Node(st, 0)); // 시작 정점을 넣는다
dist[st] = 0; // 시작 노드까지의 거리는 0
while (!pq.isEmpty()) {
Node curr = pq.poll();
if (visited[curr.v])
continue; // 이미 최단경로의 비용을 알고 있으므로 패스
visited[curr.v] = true; // 선택했다
// 현재 꺼낸 노드(curr)와 연결된 노드(node)들을 하나씩 가져자
for (Node node : adjList[curr.v]) {
if (!visited[node.v] && dist[node.v] > dist[curr.v] + node.weight) {
dist[node.v] = dist[curr.v] + node.weight;
pq.add(new Node(node.v, dist[node.v]));
}
}
}
}
static String input = "6 11\r\n" + "0 1 4\r\n" + "0 2 2\r\n" + "0 5 25\r\n" + "1 3 8\r\n" + "1 4 7\r\n"
+ "2 1 1\r\n" + "2 4 4\r\n" + "3 0 3\r\n" + "3 5 6\r\n" + "4 3 5\r\n" + "4 5 12\r\n" + "";
}'Algorithm' 카테고리의 다른 글
| [프로그래머스] 5명씩 (1) | 2023.11.24 |
|---|---|
| [프로그래머스] 공백으로 구분하기2 (1) | 2023.11.22 |
| [Java] 프림 알고리즘 & 2가지 구현방법 (반복문과 인접행렬, 우선순위큐와 인접리스트) (0) | 2022.10.23 |
| [Java] MST(최소비용신장트리) | 크루스칼 | 프림 (0) | 2022.10.17 |
| [Java] 에라토스테네스의 체 | 소수판별하기(isPrime) | 백준1929 (0) | 2022.09.20 |

